As réguas numéricas e a ideia de número par e ímpar

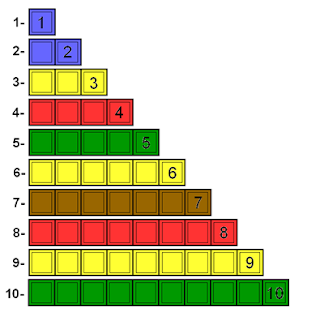
Solicite que os estudantes separem as réguas 2.

Proponha que os estudantes verifiquem quais as réguas que podem ser completadas utilizando as réguas 2 sem sobrar nem faltar nenhum quadradinho, separando essas réguas (pode-se sobrepor as réguas para melhor visualização).

Exemplo:

Peça aos estudantes que registrem no caderno os números das réguas que são completadas pela régua 2.

Peça aos estudantes que registrem no caderno os números das réguas que não são completadas pela régua 2.

Pergunte:

          “Por que, em algumas réguas, ‘faltam’ ou ‘sobram’ quadradinhos, enquanto em outras não?”

Observação: Não esqueça de trabalhar com a régua 1, para que a criança perceba que a régua 2 sobra 1 quadradinho.

Pode-se, neste momento, trabalhar o conceito de número par e número ímpar.

Atividades de comparação utilizando as réguas numéricas

Atividade 1

Proponha aos estudantes que comparem os comprimentos das peças separando uma régua de cada tamanho.

Com as réguas que foram separadas, solicite que os estudantes construam uma “escada” colocando as peças por ordem de comprimento (primeiro do menor para o maior depois do maior para o menor – ordem crescente e ordem decrescente).

Atividade 2

Solicite aos estudantes que peguem a maior e a menor régua.

Pergunte:

“Quantas réguas menores são necessárias para formar a maior?”

“Quantas vezes a peça menor cabe na maior?”

Faça essa atividade utilizando todas as réguas.

Aproveite todas as situações em sala de aula para empregar o vocabulário relativo às medidas (maior, menor, há mais, há menos, há a mesma quantidade, entre outros).

Por exemplo:

“Quantas vezes a régua 1 “cabe” na régua 10?"

 

 “Quantas vezes a régua 2 “cabe” na régua 8?"

Aproveite todas as situações em sala de aula para empregar o vocabulário relativo às medidas (maior, menor, há mais, há menos, há a mesma quantidade, entre outros).

Etapas das atividades com materiais manipulativos

          Nas atividades que são desenvolvidas com materiais manipulativos, DIENES (1972) sugere algumas etapas para serem seguidas para garantir a aprendizagem:

1.º – Noção do meio: Nesta etapa o professor deve ter bem fixo o conceito de aprendizagem como a capacidade de adaptação a um determinado meio. Ë preciso criar um meio artificial, destinado à aprendizagem de um conjunto qualquer de noções matemáticas;

2.º – Regras do jogo: Inicia-se introduzindo vários jogos, cujas regras no início são impostas, para mais tarde a criança criar as suas próprias;

3.º – Abstração: Sugere-se vários jogos semelhantes para que através das regras da etapa acima (concreta) a criança realize abstração. Mas é importante frisar que a criança ainda não tem condições de utilizar esta abstração;

4.º – Processo de representação: A criança fala do que abstraiu, na etapa acima, examina outros jogos e consegue refletir sobre estes;

5.º – Descrição da representação (linguagem): Cada criança cria sua própria linguagem, criando axiomas, e mais tarde discute com o resto do grupo qual a melhor linguagem a ser adotada;

6.º – Regras do jogo de demonstração (teoremas): Após concluir-se qual a melhor linguagem adota-se como regra. Nesta etapa pode-se dizer que a criança conseguiu atingir a noção lógica Matemática, pois formulou teoremas.

Referência:

DIENES, Z. P. As seis etapas do processo de aprendizagem em matemática. São Paulo: EPU, 1972.

 

Atividades iniciais com as Réguas Numéricas

1.ª atividade

O primeiro contato com as réguas deve ser uma brincadeira, para que os estudantes façam o reconhecimento físico da peças. Desta maneira, elas poderão perceber os atributos (cor, tamanho) do material sem que haja orientação prévia.

Peça para os estudantes construírem casinhas, pontes, pistas, trenzinhos, etc.

2.ª  atividade

O reconhecimento das cores é essencial para a compreensão das Réguas Numéricas. O avanço desta percepção, pelos estudantes, pode ser feito com a ajuda de atividades lúdicas ou jogos.

Por exemplo:

Solicite que as construções sejam feitas com cores específicas:

“Faça uma casinha utilizando somente as peças vermelhas.”

“Faça um carrinho utilizando apenas as peças amarelas.”

“Faça um trenzinho utilizando apenas as peças verdes.”

Nesta atividade as crianças serão estimuladas a observarem além do reconhecimento das cores a relação entre as cores e a numeração das réguas.

3.ª atividade

Pergunte aos estudantes o que as réguas têm de igual e de diferente.

É preciso que as crianças percebam que as réguas são diferentes na medida, tamanho, quantidade de quadradinhos, mas que algumas peças possuem a mesma cor.

Texto sobre o uso de materiais manipuláveis

O texto "Eu trabalho primeiro no concreto", de Adair Mendes Nacarato, apresenta algumas vantagens e desvantagens da utilização de materiais manipuláveis nas aulas de matemática e ressalta a importância de um planejamento adequado da atividade, no ambiente escolar, a fim incentivar o estudo dos conceitos matemáticos.

Eu trabalho primeiro no concreto

NACARATO, Adair Mendes. Eu trabalho primeiro no concreto. Revista de Educação Matemática. Sociedade Brasileira de Educação Matemática (SBEM). Ano 9, n.9-10, (2004-2005), p.1-6.

Conhecendo as peças das réguas numéricas

Um jogo de Réguas Numéricas completo possui 61 peças.

Régua 1 (azul) – 10 peças

Régua 2 (azul) – 5 peças

Régua 3 (amarelo) – 5 peças

Régua 4 (vermelho) – 5 peças

Régua 5 (verde) – 5 peças

Régua 6 (amarelo) – 5 peças

Régua 7 (marrom) – 5 peças

Régua 8 (vermelho) – 5 peças

Régua 9 (amarelo) – 5 peças

Régua 10 (verde) – 11 peças

As peças com cores iguais estabelecem uma relação de múltiplos. Manipulando as peças os estudantes desenvolvem os esquemas operatórios de adição e subtração, e ainda aprendem conceitos como “o dobro de”, ou “a metade de”, de uma quantidade.

 A régua 7 é marrom, por não possuir múltiplo diferente de 1 e dobro entre as réguas.

Um pouco sobre as réguas numéricas

As réguas numéricas foram introduzidas no Brasil no final da década de 90, com a finalidade de facilitar a compreensão da quantidade contínua para se ensinar números. Essas réguas têm repartições ao longo de sua extensão, demonstrando concretamente as quantidades descontínuas [1] dentro das contínuas [2].

As réguas numéricas darão significado aos conceitos de adição e subtração, composição dos números de 1 a 10, além de contribuir para desenvolvimento do cálculo mental.

O objetivo primordial das réguas é propiciar a decomposição dos números até 10. A exemplo, o número 8 resultará das seguintes  combinações das réguas 7 e 1, 6 e 2, 5 e 3, 4 e 4. Essas combinações deverão ser verificadas comparando-as com a régua de número 8. Ao manipular essas réguas, o aluno vivenciará a formação das adições até 10.

Nessa fase a memorização dessas adições deve ser mais sistemática. Mesmo que a criança aprenda de forma lúdica, já deve ter mais segurança nas respostas, sem ter que recorrer à contagem nos dedos ou a outros artifícios.

[1] Quantidade de natureza descontínua: o que pode ser contado.

[2] Quantidade de natureza contínua: o que pode ser medido.